Power law: universality in nature
How a simple law can explain a wide range of natural phenomena, from social networks to earthquakes
Galileo Galilei had a tough life. He was put under house arrest when he was old because he said the Earth revolved around the Sun. In 1580, when he was young, he reluctantly began studying medicine at the University of Pisa. His father wanted him to become a doctor because he didn’t see a future for his son in mathematics. Galileo was more interested in math and natural philosophy, so he focused little on his medical studies. He left Pisa in 1585 without finishing the medical course and started teaching math in Florence and later in Siena. However, his medical studies were helpful because he observed animal data and wondered why there weren’t any giant animals. We see giant gorillas climbing buildings in movies like King Kong, but why don’t they exist? Galileo figured out that more giant animals need thicker bones than smaller animals. He found a relationship between an animal’s mass (M) and size (L, length). He deduced that:
Therefore, if an animal doubles in size, its mass increases eight times. However, the bone area would only increase four times, as Galileo observed that the area S:
This means that mass increases at a faster rate than bone area. As a result, we don’t have animals larger than the blue whale, as their mass would be too great, and the pressure on their skeleton would be immense. Because of this, large animals are rarer than small ones. These relationships that Galileo discovered are examples of the power law found in various physical systems.

As the sciences continued to evolve after the Middle Ages, the power law continued to be observed. During the Scientific Revolution in the early 17th century, Johannes Kepler presented a universal law that governs the motion of celestial bodies in his book “Harmonies of the World” (“Harmonices Mundi”, in Latin), published in 1619. Using observational data from his predecessor Tycho Brahe (1546–1601), Kepler found that the square of the time (T) a planet takes to complete one orbit around the Sun is equal to the average distance of the planet to the Sun raised to the power of three (D), multiplied by a constant C. In other words, his third law establishes a mathematical relationship between a planet’s orbital period and its average distance from the Sun, which is given by:
Later, in 1687, Isaac Newton showed in his book “The Mathematical Principles of Natural Philosophy” (Philosophiae Naturalis Principia Mathematica, in Latin) that all bodies in the universe attract each other with a force that is directly proportional to their masses and inversely proportional to the square of the distance between them. This law describes how the gravitational force between two bodies varies as they move closer or farther away from each other. Mathematically, the law of universal gravitation is given by (G is a constant):
In 1785, Charles-Augustin de Coulomb also observed the relationship between force and distance. Coulomb’s law states that the electrical force between two electric charges is directly proportional to the product of their electric charges and inversely proportional to the square of the distance between them. In other words, the closer two charges are, the greater the electrical force between them, and the farther apart they are, the weaker the force. The mathematical formula for Coulomb’s law is:
Where k is the Coulomb constant, which depends on the medium in which the charges are placed.
The laws of Kepler, Coulomb, and Newton are examples of power laws, which can be expressed in the form:
The greater the value of the variable x, the smaller the function f(x) value. In the laws of Newton and Coulomb, x represents the distance between planets or charges, with α=2. Thus, the closer two planets or electric charges are, the stronger the force between them. This relationship has also been observed in the Stefan-Boltzmann Law, Stokes’ Law, self-organized criticality, and the Curie-von Schweidler Law. Moreover, it also occurs in economic, biological, and social systems, such as Pareto’s Law, which states that 80% of effects are caused by 20% of the causes, and Keibler’s Law, which relates metabolic rate to the mass of an organism. In the 19th century, Vilfredo Pareto published a work showing that about 80% of the land in Italy was controlled by 20% of the population. Recent data shows that people with extremely high incomes are rare. For example, 1% of Brazil's population holds 49% of the total income, while 80% of the poorest people concentrate only 10% of the wealth. Therefore, Pareto’s Law reflects the high social inequality observed in different countries.

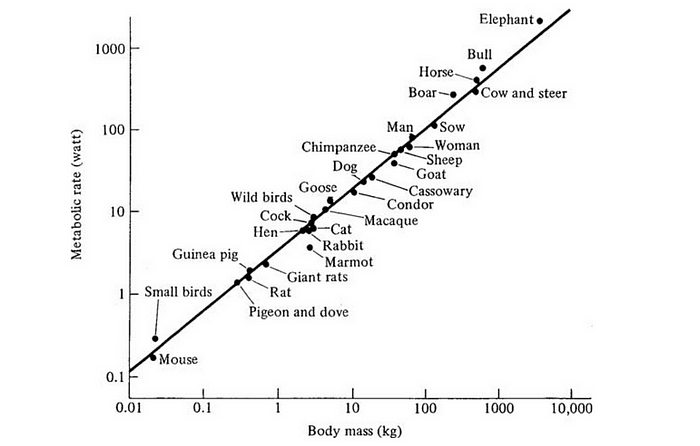
In 1932, Swiss scientist Max Keibler observed that an organism’s metabolic rate increases proportionally to its size but not in the same proportion. For instance, although an elephant is much bigger than a mouse, its metabolic rate is comparatively lower in relation to its body mass. Keibler found that a power law governs the metabolic rate with a positive exponent of 3/4. This rule has been observed in bacteria, plants, and larger animals such as mammals. Power laws have also been observed in species’ lifespan as a function of their mass (with exponent 1/4) and heart rate (with exponent -1/4). The presence of power laws in biological systems is still a mystery. Many mathematical models attempt to explain this relationship, but there still needs to be a consensus on its universality.
The laws of Kepler, Newton, and Coulomb are deterministic models in the sense that we can precisely predict the gravitational or electric force and the position of a planet at any given time. The above equation defines the power law generally, not necessarily deterministic. However, we can formulate the power law for stochastic (probabilistic) processes. In this case, f(x) represents a probability distribution. If X is a continuous random variable, for f(x) to be a probability density function, the area under f(x) must equal one. Mathematically, we can represent this as follows:
By solving this integral and calculating the constant C, we obtain the power law distribution:
The power law can also be defined for discrete random variables, and in this case, the probability of X is equal to a value x is given by:
Mathematically, the continuous case is simpler to analyze. In summary, this law states that the probability decreases with the values of x. The larger x, the less likely it is to be observed.
The power law is represented as a straight line on a log-log scale plot. That is,
As we can see from the plot below, the distribution of the population of Brazilian cities is approximately represented by a straight line when using a log-log scale plot. This plot indicates many sparsely populated cities, but few are highly populated, such as São Paulo and Rio de Janeiro, which are rare. In other words, it is not common for cities to be highly populated.

This straight line on a log-log scale is a signature of the presence of the power law. The frequency distribution of words in a book, the number of citations received by scientists, the size of lunar craters, the number of books sold, the population of cities, and the magnitude of earthquakes are examples where the power law distribution can be observed, as we can see in the following plot.

As this law is quite common, some authors suggest that the power law is even more common than the normal distribution. But why is this law so frequently observed in different systems?
“Power laws are not just a mathematical curiosity, but a key to understanding the emergent behavior of complex systems, from the Internet to the human brain.” — Steven Strogatz.
Let’s compare the power law to the normal distribution. In the normal distribution, values associated with an event are distributed around a typical value, which is its average. For example, if we measure the heights of individuals or the maximum speed of cars, we will find that the values are distributed around a typical value — the mean. Regarding heights, we should observe values around 1.70 meters, with minimum values around 1.50 meters and maximum values close to 2 meters. We will not have an individual with 0.1 or 3 meters. The same occurs with the speed of cars, which usually varies between 50 and 200 km/h. That is, we will not observe large variations between the collected values. In the case of the power law, the behaviour is different. The power law distribution arises when extreme events occur with low probability. For example, most individuals have a few hundred connections on social networks. However, there is a minority that has millions of contacts. These individuals, usually celebrities, politicians or famous athletes, are the most influential in the networks, dictating the behaviours and opinions of millions. Networks that exhibit a power law in the distribution of their connections are called scale-free networks and are present in various systems. For example, the connections between airports, proteins, routers on the Internet, and between collaborating scientists are scale-free networks. A fundamental property of the power law is the absence of a scale.

The absence of scale is related to fractals. Fractals are geometric objects that exhibit self-similarity at different scales. This means that when observed up close or from afar, they display the same structure repeated in infinitely complex patterns. Fractals are found in many natural phenomena, such as the shape of clouds, snowflakes, rivers, and mountains. They are also produced through complex mathematical equations and are used in various fields, such as modelling natural phenomena, computer graphics, and art.

This lack of scale invariance in the power law arises from a mathematical property. That is, if we replace x with dx in the previous equations, we obtain the following:
Therefore, multiplying x by a constant d does not change the shape of the distribution so we can write f(x) = g(d)f(x). The power law distribution is the only one that has this property.
Fractals are characterized by a dimension that differs from what we are used to, called the Euclidean dimension. When we look at a scene around us, we observe objects formed by three dimensions: height, length, and width. The Euclidean dimension of an object is an integer number that indicates how many times the object can be divided into equal parts and still maintain its original shape. For example, a square has a Euclidean dimension equal to 2 because it can be divided into two equal parts along its horizontal and vertical axes.
However, the fractal dimension measures the complexity of irregular objects and cannot be represented by an integer number. Instead, the fractal dimension is calculated using “box counting.” This technique involves covering the object with a grid of fixed-sized squares and counting how many of these squares contain part of the object. When we relate the number of boxes to the number of boxes that contain parts of the object, we have a power law. The exponent of this power law is related to the fractal dimension. Therefore, just as the power law shows the absence of scale, fractals exhibit self-similarity.
“A fractal is a way of seeing infinity.” — Benoit Mandelbrot.
In addition to fractals, the power law can be generated by different rules. In the case of social networks, there is an effect called “the rich get richer”. More connected individuals tend to receive more connections over time than less connected individuals. This behaviour also occurs on the Internet and in airport networks, so densely connected routers or airports usually receive more connections. The model proposed by Albert-Lazlo Barabási and Reka Albert generates scale-free networks. In this case, a vertex j will receive a connection from a vertex i according to the probability that depends on the number of connections of j; that is, if vertex j is highly connected, then it will have a higher probability of receiving a new connection. Therefore, the most connected will become even more connected — the rich will get richer… Following this rule, it is possible to show that in this Barabási and Albert model, the distribution of the number of connections is given by:
Power laws can also be generated from other processes, such as self-organized criticality, which is a state that occurs in complex systems such as climate, economy, or the human brain when they reach a delicate balance between order and randomness. In this state, small changes can lead to large consequences, and the system can adapt and evolve efficiently. It’s like a game of Jenga, where the tower is delicately balanced, and any slight movement can bring it down, but it can also lead to new tower configurations. The same happens with earthquakes, where the constant movement of the earth’s crust leads to small seismic tremors, but when enough energy accumulates, a sequence of events is triggered, leading to a large-scale earthquake. Self-organized criticality is essential in many complex systems because it allows for continuous adaptation and evolution in response to environmental changes. The power law often indicates that a system operates in a critical state of self-organized criticality. It describes how the number of events varies in relation to their magnitude.

“Due to their composite nature, complex systems can exhibit catastrophic behavior.” — Per Bak, How Nature Works: The Science of Self-organized Criticality.
Power laws also arise from energy minimization and cost minimization in information transmission. In 1932, George K. Zipf sorted the words of a book according to their occurrence and found that the frequency of occurrence is inversely proportional to their rank. The most common word has rank one, the second most common has rank two, and so on. This relationship is inversely proportional, meaning that the most frequent word occurs approximately twice as much as the second most frequent word, three times as much as the third most frequent word, and so on. The frequency of a word drops rapidly with its position in the list, following a power law distribution.

This power law among words was explained by Herbert Simon, who proposed a model in which the probability of choosing a new word to be added to a text is directly proportional to the occurrence of the word in the text written up to that point. That is, if we have a written page, the choice of the next word is proportional to its frequency in that text. Therefore, as in the case of social networks described earlier, the “rich get richer” mechanism is at work.
The power law distribution among words has important implications. Due to rare events, predicting them is a challenge, as with earthquakes. Moreover, in complex networks such as social and genetic interaction, highly connected elements, called hubs, play a fundamental role in the system’s functioning. For example, highly connected individuals are better at spreading information than those with few contacts. Thus, such hubs can efficiently propagate fake news and influence political and social debates. The same happens in our society, where highly connected individuals are the main propagators of infectious diseases. At the same time, on the internet, more connected routers concentrate a large part of the traffic. Therefore, attacking such routers can quickly fragment the network, leading to system collapse.
On the other hand, the occurrence of power laws can be beneficial. Since hubs are rare, random failures in these vertices are infrequent, thus making the network highly resilient. On the internet, routers are always disconnected, but the system continues to operate stably because the probability of removing a highly connected router is low. The same happens in biological networks, where mutations are rare among the most critical genes. Thus, the occurrence of power laws in complex networks makes the system highly robust to random failures but vulnerable to attacks. This is one of the fundamental equilibria that govern nature, where life is highly robust.
In our society and throughout history, power laws can also be observed. For example, in a recent study examining the reign of Roman emperors, we found that of the 69 emperors of the Western Roman Empire, only 24.8% reached the end of their reign peacefully and died of natural causes. The other 75.2% died violently, on the battlefield or in palace conspiracies. By modeling the life span, i.e. until suffering a violent death, we see that short reigns are the rule. A long reign is a rare event. Thus, we see that the life span of emperors follows a power law.
Although many other mechanisms generate power laws, we still need to understand how the absence of scale was favoured throughout the evolution of species. There is still much to be learned about complex systems, such as biological and social interactions, but we know that the power law is a signature of complexity in nature. Without complexity, the universe would be monotonous and without the beauty of life. Understanding power laws is understanding our universe and our origin.
Further reading:
To learn more, I suggest the book “Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies” by Geoffrey West. For more mathematical treatment, I recommend the book “Introduction to the Theory of Complex Systems,” or the review article “Power-law distributions in empirical data,” published by SIAM Review in 2009.
If you want to know more about my research, please visit this link: https://sites.icmc.usp.br/francisco.
See you next time!
